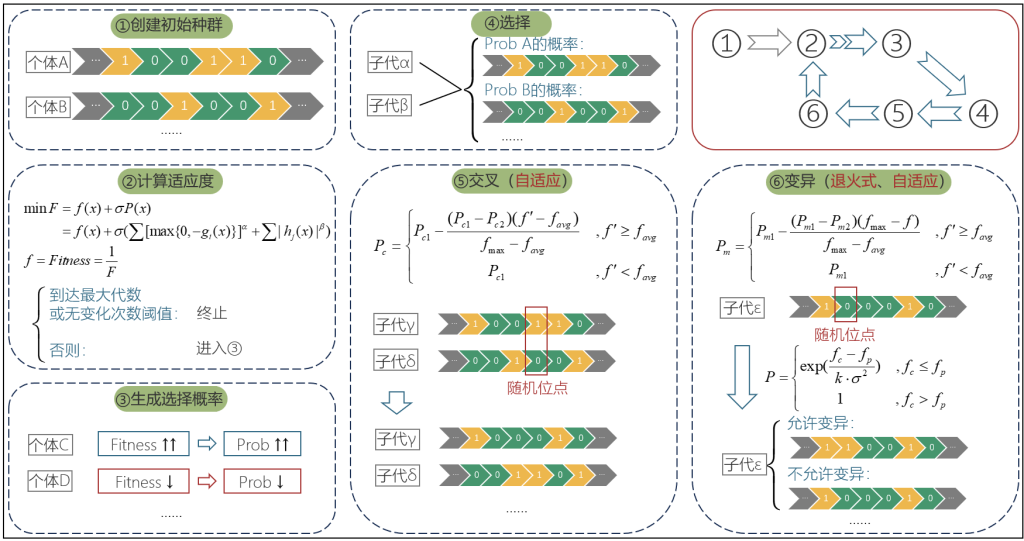
1 基本原理
遗传算法是一种随机全局搜索优化方法,模拟了生物进化中的遗传、交叉和变异等现象,通过每一代的随机交叉、变异操作,意图产生适应度更高的个体,如此循环往复,直到算法收敛,取得优良个体(问题的优质解)。
基本遗传算法的表示方法为:
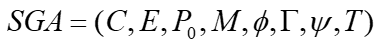
其中的元素分别代表个体的编码方案、适应度函数、初始种群、种群规模、选择算子、交叉算子、变异算子和终止条件。
- 1) 编码方案:常见的方案包括二进制编码、格雷码编码、浮点数编码等。
- 2) 适应度函数:通过当前种群在目标函数值上的表现,来表征种群的适应度大小,如果是最大化问题,适应度可以取目标函数值;如果是最小化问题,适应度可以取目标函数值的倒数。同时,在收敛后期适应度变化较小时,可以采取一定的尺度变换方法(如线性尺度变换等)扩大竞争强度,避免种群收敛于局部最优解。
- 3) 初始种群和种群规模:随机生成的包含M个个体的初始化群体。
- 4) 选择算子:从待选择的原种群中,采取一定的方法尽量选择优良的个体参加交配,以组成新种群。
- 5) 交叉算子:从种群中以一定概率(交叉概率通常为0.4 ~ 0.99)随机选择一对或多对个体,交换部分特征,意图将父代的优秀特征遗传给子代。交叉方法包括单点交叉、多点交叉等。
- 6) 变异算子:从种群中以一定概率(突变概率通常为0.001 ~ 0.1)随机选择个体进行变异(通常为单点变异)操作,产生新的特征,以防止收敛陷入局部最优。
- 7) 终止条件:如果算法收敛,或是达到了预设的迭代次数上限,则算法终止,导出当前为止的最优解。
2 改进思路
2.1 输入项的类型扩展
将输入的待优化参数x从单独的连续型变量或离散型变量,扩展为二者的混合。即输入x既可以是一定范围内的连续值,也可以是一定范围内的离散值。与此同时,目标函数中以罚函数形式构成的约束条件也支持混合型的x取值。
2.2 自适应交叉、突变概率
在传统遗传算法中,交叉概率和变异概率都是固定的,这会在一定程度上影响算法的效率。为了使得遗传算法的思路更加适合寻求优良个体,需要对交叉概率和突变概率的给定方式进行改进。改进的目标为:
- 1) 对于已通过适应度识别出的优良个体,应该尽量保留其优良特性,交叉概率和变异概率都应减小;反之,对于劣质个体,应该增大交叉概率和变异概率。
- 2) 在接近收敛的迭代中,已经不再需要和前期一致的较高的交叉概率和变异概率,相反地,后期迭代应该尽量控制交叉和变异的范围,使得找到最优解后种群能快速收敛。
M. Srinivas和L. M. Patnaik提出的AGA(自适应遗传算法)给出了相应的改进方法,自适应的交叉概率P_c和变异概率P_m的表达式分别为
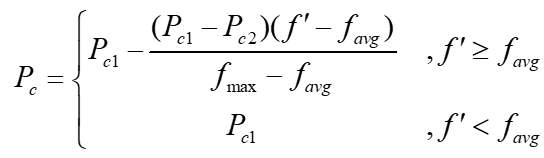
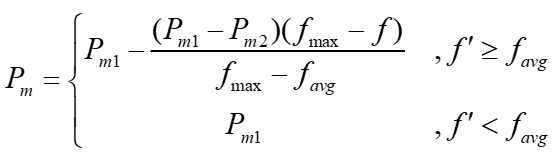
其中,f_max表示这一代种群中的最大适应度,f_avg表示这一代种群的平均适应度,f'表示两个需要交叉的个体中,更优良个体对应的适应度,f表示待突变个体的适应度。对于参数P_c1, P_c2, P_m1, P_m2的取值,为避免优良个体在收敛前期快速繁殖导致种群早熟,建议取值为P_c1 = 0.9, P_c2 = 0.6, P_m1 = 0.1, P_m2 = 0.001。
2.3 自适应退火式变异
将模拟退火算法中的退火概率引入遗传算法的变异过程,当变异导致适应度降低时,用退火概率判定是否保留变异特征。其目的是减少迭代次数,从而进一步提高算法的效率,同时在一定程度上避免种群早熟。
引入退火概率的具体流程为:
- 1) 在待突变个体执行变异操作前,记录此时的种群特征,之后执行变异操作;
- 2) 计算该突变个体在变异前后的适应度f_p和f_c;
- 3) 计算突变后当前种群个体适应度的样本方差,即
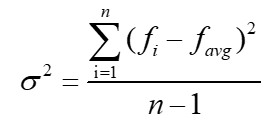
- 4) 根据自适应的退火概率设定公式求当前的退火概率,即
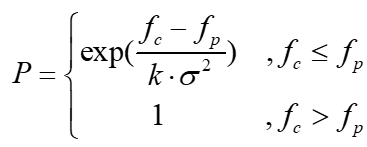
- 其中k为常数,根据实际问题调整大小;
- 5) 得到的退火概率即为变异操作的保留概率,如果判定为保留,则维持当前种群特征;如果判定为不保留,则利用事先记录的原种群特征对当前种群进行还原。
3 附录:模型代码
3.1 ASA-AGA类(改进GA类)
原始GA模型代码取自CSDN某位大神对Python的sko.GA库里GA函数的优化,这一优化方法本身性能就很强悍:输入的x可以是离散变量和连续变量的混合体。但是原链接失效了(悲),博主无法设置跳转大神博客。而博主根据自适应和退火思想的改进基于此代码进行。
class GeneticAlgorithm(object):
"""
遗传算法, 用于求解非线性数值优化问题
Note:
1. 优化问题的输入X可以是连续值、离散类别或者二者混合, 输出y也可以是两种类型混合
2. GA算法本身原理是不含约束的, 如果求解问题中含有约束, 可以从以下方式解决:
* 对自变量X约束, 可以在chrome_bounds中设定对应被约束变量的上下界边界值
* 对输出y约束, 可以对应约束条件利用y输出值构造惩罚函数, 惩罚函数中构造了
约束边界的梯度, 这样样本点会在迭代过程中沿着约束梯度方向划入可行域
"""
def __init__(self, chrome_len, chrome_bounds, chrome_types, pop_size):
"""
初始化
:param chrome_bounds: list of lists, 染色体上各位置取值范围, 连续值对应上下界, 离散值对应所有可能取值情况
:param chrome_types: list of ints from [0, 1], 用于标记染色体上各个元素数据类型,1为连续,0为离散
:param chrome_len: int, 染色体长度,对应待优化参数维数
:param pop_size: int, 种群数量
"""
if (len(chrome_bounds) != chrome_len) | (len(chrome_types) != chrome_len):
raise ValueError('边界或类型设置与维数不一样长')
self.chrome_len = chrome_len
self.chrome_bounds = chrome_bounds
self.chrome_types = chrome_types
self.pop_size = pop_size
self._init_pop()
def _gen_rand_values(self, i):
"""产生第i列的随机量"""
rand_values = None
col_bounds, col_type = self.chrome_bounds[i], self.chrome_types[i]
if col_type == 1:
rand_values = np.random.random(self.pop_size)
rand_values = rand_values * \
(col_bounds[1] - col_bounds[0]) + col_bounds[0]
elif col_type == 0:
rand_values = np.random.choice(col_bounds, self.pop_size)
rand_values = rand_values.reshape(-1, 1)
rand_values = np.array(rand_values, dtype=np.float32)
return rand_values
def _init_pop(self):
"""
初始化种群
:param chrome_bounds: refer to the definition of chrome_bounds in __init__(self)
:param chrome_bounds: refer to the definition of chrome_bounds in __init__(self)
"""
for i in range(self.chrome_len):
col_bounds, col_type = self.chrome_bounds[i], self.chrome_types[i]
if col_type == 1: # 连续值
if (len(col_bounds) != 2) | (col_bounds[0] >= col_bounds[1]):
raise ValueError('第{}个变量为连续数值,其边界参数不正确'.format(i))
elif col_type == 0: # 离散值
pass
else:
raise ValueError('数值类型参数有误')
self.pop = None
for i in range(self.chrome_len):
col_rand_values = self._gen_rand_values(i)
if i == 0:
self.pop = col_rand_values
else:
self.pop = np.hstack((self.pop, col_rand_values))
def _cal_fitness(self, func, optim_direc, normalize=True):
"""
计算适应度
:param obj_func: function, 目标函数
:param optim_direc: str from {'minimize', 'maximize'}, 优化方向
:param normalize: bool, 是否进行0-1归一化处理
:return: fitness, normalized_fitness(or fitness if not normalized)
"""
fitness = np.apply_along_axis(func, 1, self.pop)
if optim_direc == 'minimize':
fitness = 1 / fitness
elif optim_direc == 'maximize':
pass
else:
raise ValueError('optim_direc参数不正确')
if normalize:
min_fit, max_fit = np.min(fitness), np.max(fitness)
if min_fit == max_fit:
normalized_fitness = np.ones_like(fitness)
else:
normalized_fitness = (fitness.copy() - min_fit) / (max_fit - min_fit)
return fitness, normalized_fitness
else:
return fitness, fitness
@staticmethod
def _get_accum_prob(fitness):
r"""
将适应度转化为累计概率
:param fitness: np.array, 一维适应度表序列
:return: accum_prob: np.array, 一维累计概率表
"""
accum_fitness = fitness.copy()
for i in range(len(fitness) - 1):
accum_fitness[i] = np.sum(fitness[: i + 1])
accum_fitness[-1] = np.sum(fitness)
accum_prob = accum_fitness / (accum_fitness[-1])
return accum_prob
def _gen_children(self, accum_prob):
r"""
根据累积概率表生成同样规模的子代种群
:param accum_prob:
"""
rand_nums = np.random.random(self.pop_size)
children_nums = []
for i in range(len(rand_nums)):
num = rand_nums[i]
if num <= accum_prob[0]:
children_nums.append(0)
else:
for j in range(len(accum_prob) - 1):
if accum_prob[j] < num <= accum_prob[j + 1]:
children_nums.append(j + 1)
self.pop = self.pop[children_nums, :]
def _cross_over(self, best_fitness, avg_fitness, fitness):
"""交配, 相邻样本随机交换元素"""
for i in range(self.pop_size - 1):
# 新增功能1:自适应交换概率
sub_fitness = np.max(fitness[i: i + 1])
# pc_dynamic = (best_fitness - sub_fitness) / (best_fitness - avg_fitness)
pc_dynamic = 0.9 - 0.3 * (sub_fitness - avg_fitness) / (best_fitness - avg_fitness)
if avg_fitness > sub_fitness:
# pc_dynamic = 1
pc_dynamic = 0.9
if abs(best_fitness) > 1e6 or np.random.random() < pc_dynamic:
cpoint = np.random.randint(0, self.chrome_len)
self.pop[i, cpoint], self.pop[i + 1,
cpoint] = self.pop[i + 1, cpoint], self.pop[i, cpoint]
def _mutate(self, best_fitness, avg_fitness, fitness, obj_func, optim_direc, normalize):
"""突变,随机样本随机位点突变"""
for i in range(self.pop_size):
# 新增功能2:自适应突变概率
sub_fitness = fitness[i]
# pm_dynamic = 0.5 * (best_fitness - sub_fitness) / (best_fitness - avg_fitness)
pm_dynamic = 0.1 - 0.099 * (best_fitness - sub_fitness) / (best_fitness - avg_fitness)
if avg_fitness > sub_fitness:
# pm_dynamic = 0.5
pm_dynamic = 0.1
if abs(best_fitness) > 1e6 or np.random.random() < pm_dynamic:
mpoint = np.random.randint(0, self.chrome_len)
bounds, type = self.chrome_bounds[mpoint], self.chrome_types[mpoint]
pre_pop = self.pop[i, mpoint]
if type == 1:
self.pop[i, mpoint] = np.random.random(
) * (bounds[1] - bounds[0]) + bounds[0]
elif type == 0:
self.pop[i, mpoint] = np.random.choice(bounds)
# 新增功能3:自适应退火式变异
re_fitness, re_nmlzd_fitness = self._cal_fitness(obj_func, optim_direc, normalize)
if re_fitness[i] < fitness[i]:
var_fitness = np.var(fitness, ddof=1)
if var_fitness == 0:
var_fitness = np.var(fitness[: -1] + [fitness[-1] * (1 - 1e-5)], ddof=1) # 防止0除报错
prob_sa = np.exp((re_fitness[i] - fitness[i]) / (100 * var_fitness)) # 取样本方差的倍数
# prob_sa = np.exp((re_fitness[i] - fitness[i]) / var_fitness)
if np.random.random() < prob_sa:
self.pop[i, mpoint] = pre_pop
def _best_individual(self, fitness):
"""获取最优个体和对应的适应度"""
best_fitness = np.max(fitness)
avg_fitness = np.mean(fitness) # 新增功能:导出平均适应度
best_individual = self.pop[np.argmax(fitness), :].reshape(
1, -1)[0, :] # **防止有多个最优解
return best_fitness, best_individual, avg_fitness
@time_cost
def evolution(self, obj_func, optim_direc: str, epochs: int, max_no_change: int, normalize: bool = True,
fit_adj_func=_exp_adj_func, verbose: bool = True, plot: bool = False) -> Tuple[float, list, list]:
"""
执行进化
:param fit_adj_func: func, 函数对象, 用于对适应度进行非线性调节以计算对应概率
:param normalize: bool, 是否对fitness值进行min-max归一化
:param obj_func: function, 优化目标函数
* 如果待优化问题包含约束条件, 则写成lambda x: obj_func(x) + constr_func(x)的形式(罚函数法)
* 约束条件函数必须为 f(x) = 0的隐函数格式, 且使用python基本运算编写, 否则符号函数运算容易报错
:param optim_direc: str from {'minimize', 'maximize'}, 优化方向
:param epochs: int, 优化步数
:param max_no_change: int, 最长无改变次数
:param verbose: bool, 是否打印学习过程
:param plot: bool, 是否导出最优适应度变化图象
:return:
final_fitness: float, 最终适应度
final_individual: list of floats or ints, 最终筛选出的个体
eval_process: list, 进化过程记录
"""
eval_process = []
global_best_fitness, global_best_individual = None, None
no_change = 0
df_best_fitness = pd.DataFrame(columns=['epoch', 'global_best_fitness', 'current_best_fitness'])
for epoch in range(epochs):
# 计算当前最优适应度和最优个体
fitness, nmlzd_fitness = self._cal_fitness(obj_func, optim_direc, normalize)
best_fitness, best_individual, avg_fitness = self._best_individual(fitness)
if best_fitness == avg_fitness:
avg_fitness -= 1e-5 * best_fitness # 防止0除报错
if epoch == 0:
global_best_fitness, global_best_individual = best_fitness, best_individual.copy()
else:
if best_fitness > global_best_fitness:
global_best_fitness, global_best_individual = best_fitness, best_individual.copy()
# 记录当前最佳适应度用于制表
df_best_fitness.loc[len(df_best_fitness)] = [epoch, global_best_fitness, best_fitness]
# 记录进化过程
if verbose and epoch % 10 == 0:
print('epoch: {}, global_best_fitness: {:.6f}'.format(
epoch, global_best_fitness))
eval_process.append(
[global_best_fitness, list(global_best_individual)])
# 执行遗传、交配和变异
adj_fitness = fit_adj_func(nmlzd_fitness)
accum_prob = self._get_accum_prob(adj_fitness)
self._gen_children(accum_prob)
self._cross_over(best_fitness, avg_fitness, fitness)
self._mutate(best_fitness, avg_fitness, fitness, obj_func, optim_direc, normalize)
# 查看优化结果是否有明显改变
if epoch > 0:
if eval_process[-1][0] == eval_process[-2][0]:
no_change += 1
else:
no_change = 0
if no_change == max_no_change:
print('Reaching the max_no_change number, break the loop')
break
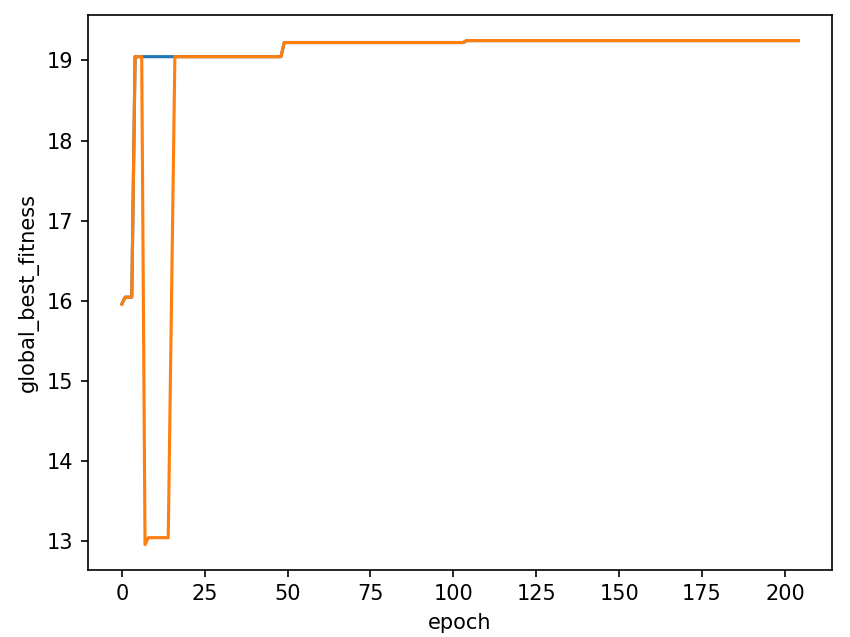
# 输出图像
if plot:
sns.lineplot(data=df_best_fitness, x='epoch', y='global_best_fitness')
sns.lineplot(data=df_best_fitness, x='epoch', y='current_best_fitness')
plt.show()
final_fitness, final_individual = eval_process[-1]
return final_fitness, final_individual, eval_process3.2 其他函数
模型库导入及初始设置:
import logging
import os
logging.basicConfig(level=logging.INFO)
os.environ['NUMEXPR_MAX_THREADS'] = '16'
from typing import Tuple
from lake.decorator import time_cost
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd初始值x的非线性调整,使之标准化:
def _exp_adj_func(x, w=10.0):
"""
非线性调整项,将数值映射到0-1区间
"""
x = (np.exp(w * x) - 1.0) / (np.exp(w) - 1)
return x定义罚函数:
# 定义罚函数的格式,并且提供两个模式
def constr_func(func, mode='ueq', direc='minimize', sigma=1e6):
sigma = sigma if direc == 'minimize' else - sigma
if mode == 'ueq': # 不等式约束
return 0 if func <= 0 else sigma
elif mode == 'eq': # 等式约束
return 0 if func == 0 else sigma
else:
raise TypeError('罚函数的模式输入错误')遗传算法本身的原理中是不含约束的,博主的方案是通过构造罚函数解决约束规则的表达问题。
3.3 引用改进GA类的说明
目标函数表达
如果目标函数是求负,需要变为求正(min变号转max or max变号转min)。如果本身目标函数就是求正,那么原始的min和max不需要变换,靠后续的direc, optim_direc参数调控优化方向即可。
约束条件
表达约束条件时需要注意:
- 对于约束条件,确保式子转化为g(x) <= 0或h(x) = 0的形式,需要表达的格式即为左侧的x函数g(x)或h(x)。
- 如果同类约束条件只有一个,可以直接填写表达式;如果同类约束条件有多个,需要将表达式用元组整合起来。
- 等式约束条件可能需要注意参数的整型化。
例如:
# 加入一个等式约束条件:x[1] + x[2] == 1.5
constr_eq = round(x[1] + x[2], 1) - 1.5
# 加入两个不等式约束条件:
constr = (
9 * x[0] + 7 * x[1] - 56,
7 * x[0] + 20 * x[1] - 70
)目标函数返回值
返回值应为目标函数值与罚函数值之和,用于指导模型调参。引用罚函数方法constr_func()时需要注意,该方法默认的约束条件格式为不等式,默认的返回值方向为最小化(mode='ueq', direc='minimize'),因此如果约束条件中含有等式,或目标函数为极大化,则需要设置对应的参数。
例如:
# 目标函数为极大化
return func + sum(constr_func(constr[i], direc='maximize') for i in range(len(constr)))
# 约束条件中含有等式
return func + constr_func(constr_1) + constr_func(constr_2, mode='eq')其他参数设置
- chrome_len: x变量的个数。
- chrome_bounds: x变量的取值范围,为嵌套列表格式,单个列表中的元素为区间两端点(连续变量)或取值集合中的所有元素(离散变量)
,这时就有人会问了,区间不止一个怎么办?请善用不等式约束条件作为替代方案。 - chrome_types: x变量的类型,1为连续变量,0为离散变量。
- pop_size: 种群数量,建议取20以上。
- optim_direc: 优化方向,'minimize'表示极小化,'maximize'表示极大化。
- epochs: 迭代的轮数。
- max_no_change: 多少轮无变化后迭代终止,建议这个值填大一点。
3.4 引用示例
示例1:如何同时引入离散和连续的x变量
问题:求向量x = [x_1, x_2, x_3]的最小二范数近似值,其中x_1为连续变量,取值区间[-1, 0];x_2为离散变量,取值区间{0.5, 1, 2, 3};x_3为离散变量,取值区间为{-1.1, 1, 1.2}。变量之间存在约束条件:x_1 <= -0.02;x_2 + x_3 == 1.5。
引用方法:
# 目标函数
def min_obj_func(x):
# 表达出目标函数 min f
func = np.linalg.norm(x, 2)
# 加入一个不等式约束条件:x[0] <= -0.02
constr_1 = x[0] + 0.02
# 再加入一个等式约束条件: x[1] + x[2] == 1.5
constr_2 = round(x[1] + x[2], 1) - 1.5
return func + constr_func(constr_1) + constr_func(constr_2, mode='eq')
# 设定参数
chrome_len = 3
chrome_bounds = [[-1, 0], [0.5, 1, 2, 3], [-1.1, 1, 1.2]]
chrome_types = [1, 0, 0]
pop_size = 100
optim_direc = 'minimize'
epochs = 100
max_no_change = 5
# 进行遗传算法规划
ga = GeneticAlgorithm(chrome_len, chrome_bounds, chrome_types, pop_size)
final_fitness, final_individual, _ = ga.evolution(
min_obj_func,
optim_direc=optim_direc,
epochs=epochs,
max_no_change=max_no_change
)
print('{}_f_value: {:.6f}'.format(optim_direc, final_fitness))
print('final_individual: {}'.format(final_individual))示例2:如何表达最大化问题
问题:
目标函数:
max z = 3x_1 + x_2 + 3x_3 + 3
约束条件:

引用方法:
def min_obj_func(x):
# 表达出目标函数 max f
func = 3 * x[0] + x[1] + 3 * x[2] + 3
# 不等式约束条件
constr = (
- x[0] + 2 * x[1] + x[2] - 4,
4 * x[1] - 3 * x[2] - 2,
x[0] - 3 * x[1] + 2 * x[2] - 3
)
return func + sum(constr_func(constr[i], direc='maximize') for i in range(len(constr)))
# 设定参数
chrome_len = 3
chrome_bounds = [[i for i in range(10)], [0, 10], [0, 1]]
chrome_types = [0, 1, 0]
pop_size = 100
optim_direc = 'maximize'
epochs = 1000
max_no_change = 100
# 进行优化
ga = GeneticAlgorithm(chrome_len, chrome_bounds, chrome_types, pop_size)
final_fitness, final_individual, _ = ga.evolution(
min_obj_func,
optim_direc=optim_direc,
epochs=epochs,
max_no_change=max_no_change,
verbose=True,
plot=True
)
print('{}_f_value: {:.6f}'.format(optim_direc, final_fitness))
print('final_individual: {}'.format(final_individual))作图: