1 基本描述
当下,车辆轨迹预测拥有较为宽广的应用场景:
一般的车辆轨迹预测技术通常用于提高交通流畅度、减少事故发生率以及优化路网利用率等目的。例如,交通运输企业可以利用车辆轨迹预测技术来优化路线规划,使车辆能够更高效地完成配送任务。同时,交通管理机构也可以利用车辆轨迹预测来制定交通管制措施,提高道路利用效率,缓解交通拥堵等问题。
而实时的轨迹预测通常用于辅助车辆行驶,比如汽车导航系统可以利用实时轨迹预测技术来提供实时的路线规划和交通警告等功能。此外,实时轨迹预测还可以用于交通监控,能够帮助交通管理机构快速发现并应对交通事故、拥堵等突发情况。
本报告所设计的功能模块,提供了一种基于LSTM(长短期记忆递归神经网络)算法的车辆轨迹实时预测思路。以下是对LSTM算法的简要介绍:
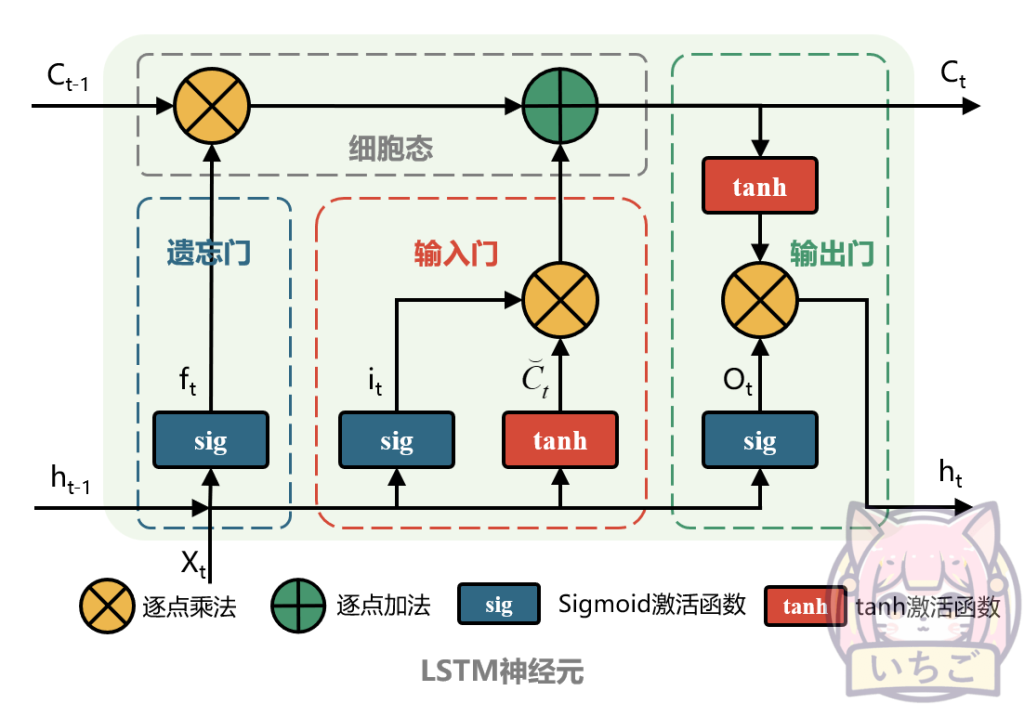
LSTM是一种适用于在重要事件之间的未知大小和持续时间的时间延迟上分类、处理和预测时间序列的递归神经网络。 LSTM特别适用于从序列数据学习,因为它们允许模型在学习后面的时间步骤时保留来自早期时间步骤的信息。
LSTM通过使用三种不同类型的门来控制信息流来工作:输入、输出和遗忘门。输入门确定应该将当前时间步的哪些信息传递到下一个时间步,输出门确定应该输出当前时间步的哪些信息,而遗忘门确定应该丢弃从上一个时间步传来的哪些信息。通过这些门,LSTM可以有选择地记住或忘记过去的信息,并使用这些信息对未来进行预测。 LSTM在自然语言处理任务中广泛使用,例如语言翻译、文本摘要和文本分类。它们还用于其他领域,如音乐生成和财务预测。本文的轨迹预测涉及到时序信息,同样是LSTM的应用场景。
2 需求分析
使用开源数据集NGSIM进行研究。NGSIM的全程为Next Generation Simulation,是隶属美国联邦公路局的数据采集项目,被广泛用于车辆跟驰换道等驾驶行为研究,交通流分析,自动驾驶决策规划等交通领域研究中。
原始数据为美国高速公路国道101的实时车辆运行轨迹数据,数个文档对应不同时段,每个时段为15分钟。经分析,原始数据中本模块可能用到的字段意义如表2.1所示。

观察可知,若需要将特定编号的车辆从原始数据中找出,并对其进行轨迹预测,则需要先筛选出其编号索引下所有的数据行,再将所有行依照时刻先后进行排序,最后整理出一段或多段连续的轨迹。
以Vehicle_ID=515的小汽车为例,数据整理操作如下:
1) 从原始数据中随机抽取Vehicle_ID,得到“515”;
2) 将所有Vehicle_ID=515的数据行找出;
3) 将2)中获取的数据行按照Global_Time进行排序,使其递增;
4) 在时序递增的条件下,找到间断点并拆分不同时间段的轨迹;
5) 将每条轨迹改为从moment=0开始,但同时记录原始的开始时间。
在完成该小汽车的全部轨迹数据整理后,着手开始轨迹预测流程。轨迹预测需要重点用到车辆的Local_X和Local_Y数据,依据原始数据的描述信息,前者指道路中心线与车辆前部中心点的垂线长度(即车辆与道路中心线的间距,可作为X轴),后者指道路参照线与车辆前部中心点的垂线长度(即车辆与研究区段起点的距离,可作为Y轴)。
经分析,LSTM模型在轨迹预测中主要有两点优势:
在轨迹预测中,LSTM模型可以利用车辆之前的行驶轨迹来预测未来轨迹。由于LSTM模型能够记忆长期依赖关系,因此在预测未来轨迹时能够考虑到车辆之前的行驶轨迹,这使得LSTM在轨迹预测中具有很好的表现。
此外,LSTM模型还具有较强的泛化能力,能够很好地适应新的数据。在轨迹预测中,这意味着LSTM模型能够很好地适应不同的道路环境、交通流量等情况,并能准确预测车辆的未来轨迹。
因此,本研究将尝试使用LSTM模型对车辆轨迹进行预测。为了尽可能确保模型在预测时的精确性,采取的主要思路如下:
- 1) 数据清洗、拆分和结构优化:主要包含归一化、查找异常点并删除、构建轨迹数组并降维、构建时刻数组、创建差值数据集等步骤;
- 2) 数据训练与结果输出:主要包含数据训练、计算均方差、建立优化器、趋势预测、结果可视化等步骤。 具体的技术流程详见第四节(详细设计)部分。
3 系统流程
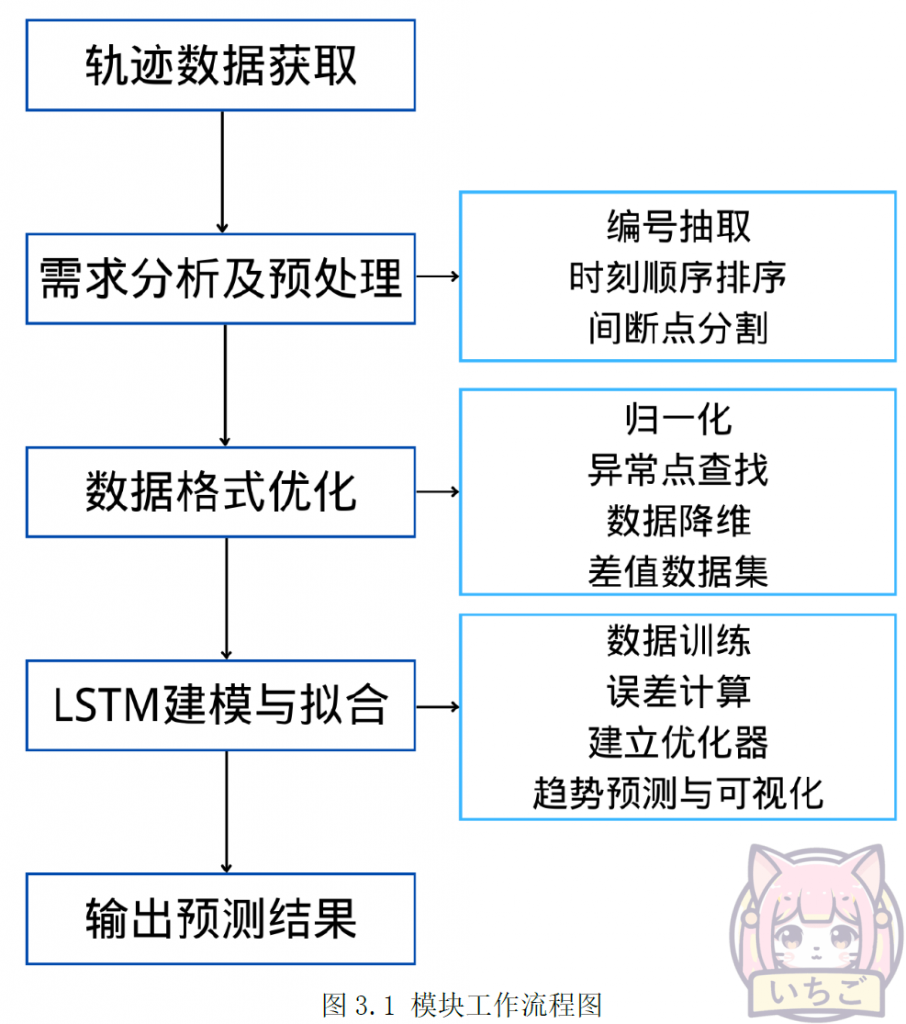
模块的工作流程如图3.1所示。主要包含轨迹数据获取、需求分析及预处理、数据格式优化、LSTM建模与拟合、输出预测结果5个部分。
4 详细设计
本部分为LSTM车辆轨迹预测模型的详细建模过程设计。
A. 数据清洗、拆分和结构优化
a. 归一化
数据处理的第一步即为归一化操作,本模型采用模型训练中常见的最大最小归一化方法,即:利用数据列中的最大值和最小值进行标准化处理,计算方式为数据与该列的最小值作差,再除以极差。
b. 查找异常点并删除
在归一化完成后,利用3-sigma原则(即去除分布中位于两端的统计学小概率值),查找数据中存在的异常点并删除。
c. 构建数组
为确保后续预测的精度并降低算法的计算开销,轨迹数组需要进行降维处理。本模型采用PCA降维算法进行数据降维。PCA算法为主成分分析算法,在数据集中找到“主成分”,可以用于压缩数据维度。该算法的主要流程为:去均值化,使数据中心位于零点;计算数据的协方差矩阵;计算特征值和特征向量;对数据进行降维。计算所得的协方差矩阵、特征值和特征向量可以在后续用于还原预测结果的维度。
在对轨迹数组X进行降维并归一化之后,再构建时刻数组Y。
d. 创建数据集
为了方便LSTM模型中batch_size的设置,需要控制数据集长度为2的某次方项的倍数,这样可以设置尽可能多的batch_size。本模型中令数据集长度为16的倍数,则batch_size在调试时可以设置为1、2、4、8、16。
在创建数据集时,除了直接整合X、Y数据之外,还可以创建差值数据集,将轨迹数组X相邻项的差值作为新的自变量,进一步提高模型的预测精度。但后续结果表明,计算差值之前的数据集预测效果已经良好,故最终没有使用此方案。
B. 数据训练与结果输出
a. 参数设置
数据训练过程中有大量的模型参数需要进行调整,如表4.1所示。表中的设置值是大量尝试后确定的值,在设置值的条件下运行模型可以尽可能维持较高的精度和运行效率。

在上述模型参数中,对模型精度影响较大的有batchSize和leaningRate。每次抓取的样本量(batchSize)越多,模型建立前后联系就越准确,但同时也会大幅增加运算量;学习率(leaningRate)如果太大,容易导致欠拟合,而太小又容易出现过拟合现象,因此本模型中采用了学习率指数衰减的处理方法,使得学习率会随着训练循环数的增加,从一个较大的值逐步衰减到一个较小的值,提高模型的拟合速度并减少过拟合、欠拟合现象的发生。
b. 模型的整体结构
LSTM模型是较为复杂的神经网络模型,实现步骤较多,如表4.2所示。

在规划好模型的整体结构后,即进入编码开发环节,代码详见报告第五节。
5 编码开发
相关代码的编写在Python语言框架下进行。使用的方法库概述如表5.1所示。

代码全文如下:
# 基于LSTM算法的车辆轨迹预测
# Developed by: gpluo
import pandas as pd
import numpy as np
import csv
import os
import matplotlib.pyplot as plt
import torch
from torch import nn
from sklearn.preprocessing import MinMaxScaler
# 创建文件夹
def dicBuild(path):
# 去除首位空格
path = path.strip()
isExists = os.path.exists(path)
if not isExists:
os.makedirs(path)
# 创建CSV文件
def csvBuild(path, mat):
file = open(path, mode='w', encoding='utf-8', newline='')
csvWriter = csv.DictWriter(file, fieldnames=['Global_Time', 'Local_X', 'Local_Y'])
csvWriter.writeheader()
for item in mat:
dit = {
'Global_Time': item[0],
'Local_X': item[1],
'Local_Y': item[2]
}
csvWriter.writerow(dit)
file.close()
# 原始数据加载
def loadOrg(vehicleID):
dfOrg = pd.read_csv('Next_Generation_Simulation__NGSIM__Vehicle_Trajectories_and_Supporting_Data.csv')
matOrg = np.array(dfOrg[['Vehicle_ID', 'Global_Time', 'Local_X', 'Local_Y']]).tolist()
matTotalOrg = []
for item in matOrg:
if int(item[0]) == vehicleID:
matTotalOrg.append([int(item[1]), float(item[2]), float(item[3])])
# 对原始的时刻进行排序,使其递增
matTotal = sorted(matTotalOrg, key=lambda ele: ele[0])
# 在递增的条件下,找到间断点并拆分不同时间段的轨迹
matTotal3D = []
matFinalItem = matTotal[-1] # 标记终点用于结束循环
while True:
if len(matTotal) <= 1:
break
matTotal3DEle = []
for i in range(len(matTotal) - 1):
matTotal3DEle.append([matTotal[i][0], matTotal[i][1], matTotal[i][2]])
# 拆分:间断点或终点
if ((matTotal[i + 1][0] - matTotal[i][0]) > 100) or (matTotal[i + 1] == matFinalItem):
matTotal3D.append(matTotal3DEle)
del matTotal[: i + 1]
break
# 去除重复数据
elif (matTotal[i + 1][0] - matTotal[i][0]) == 0:
i += 1
# 每条轨迹改为从moment=0开始
for matItem in matTotal3D:
timeMin = matItem[0][0]
for item in matItem:
item[0] -= timeMin
print('complete')
return matTotal3D
# 数据降维:PCA算法
def methodPCA(arrayOrg):
def plotScatter(arrayDeMean, recoveredArray):
fig, ax = plt.subplots(figsize=(10, 10))
ax.scatter(arrayDeMean[:, 0], arrayDeMean[:, 1])
ax.scatter(list(recoveredArray[:, 0]), list(recoveredArray[:, 1]), c='r')
ax.plot([arrayDeMean[:, 0], list(recoveredArray[:, 0])], [arrayDeMean[:, 1], list(recoveredArray[:, 1])])
plt.show()
# 去均值化
def deMean(arrayOrg):
arrayDeMean = (arrayOrg - np.mean(arrayOrg, axis=0))
return arrayDeMean
# 计算数据的协方差矩阵
def sigmaMat(arrayDeMean):
sigma = (arrayDeMean.T @ arrayDeMean) / arrayDeMean.shape[0]
return sigma
# 计算特征值、特征向量
def usv(sigma):
u, s, v = np.linalg.svd(sigma)
return u, s, v
# 对数据进行降维
def dimReduction(arrayDeMean, u, k):
reducedU = u[:, :k]
z = np.dot(arrayDeMean, reducedU)
return z
# 数据还原
def dataRecover(z, u, k):
reducedU = u[:, :k]
recoveredArray = np.dot(z, reducedU.T)
return recoveredArray
arrayDeMean = deMean(arrayOrg)
sigma = sigmaMat(arrayDeMean)
u, s, v = usv(sigma)
z = dimReduction(arrayDeMean, u, 1)
# 数据还原方法
# recoveredArray = dataRecover(z, u, 1)
# 降维前后对比
# plotScatter(arrayDeMean, recoveredArray)
return arrayDeMean, z, u
# 3sigma原则查找异常点并删除
def threeSigma(dfCol): # dfCol: 数据的某一列
rule = (dfCol.mean() - 3 * dfCol.std() > dfCol) | (dfCol.mean() + 3 * dfCol.std() < dfCol)
index = np.arange(dfCol.shape[0])[rule]
outrange = dfCol.iloc[index]
return outrange
# 定义LSTM算法
class LSTMRNN(nn.Module):
"""
Parameters:
- input_size: feature size
- hidden_size: number of hidden units
- output_size: number of output
- num_layers: layers of LSTM to stack
"""
def __init__(self, input_size, hidden_size=1, output_size=1, num_layers=1):
super().__init__()
self.lstm = nn.LSTM(input_size, hidden_size, num_layers) # utilize the LSTM model in torch.nn
self.forwardCalculation = nn.Linear(hidden_size, output_size)
def forward(self, _x):
x, _ = self.lstm(_x) # _x is input, size (seq_len, batch, input_size)
s, b, h = x.shape # x is output, size (seq_len, batch, hidden_size)
x = x.view(s * b, h)
x = self.forwardCalculation(x)
x = x.view(s, b, -1)
return x
# 训练函数
def trainCore(dataset):
# 预测结果可视化
def resultPlot():
plt.figure()
plt.plot(tForTraining, trainY, 'b', label='locTRN') # 训练集原曲线
plt.plot(t[trainLength:], testY[trainLength:], 'k', label='locTST') # 测试集原曲线
plt.plot(tForTest, predictiveYTest, 'm--', label='preLocTST') # 预测曲线
plt.plot([t[trainLength], t[trainLength]], [0, 1], 'r--', label='separation line') # 训练集、测试集分界线
plt.xlabel('t')
plt.ylabel('locVar')
plt.xlim(t[0], t[-1])
plt.ylim(0, 1)
plt.legend(loc='best')
plt.grid()
plt.show()
# 确认GPU运算是否可行
device = torch.device("cpu")
if torch.cuda.is_available():
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
device = torch.device("cuda:0")
print('Training of GPU.')
else:
print('No GPU available, training on CPU.')
# 参数设置
trainRatio = 0.95 # 训练集占比的约数
batchSize = 16 # 每次抓取的样本数量
inputFeaturesNum = 1 # 输入维度
outputFeaturesNum = 1 # 输出维度
hiddenSize = 64 # 隐含层的特征维度
numLayers = 3 # 隐含层的层数(默认为1)
maxEpochs = 10000 # 最大训练循环数
learningRate = 1e-2 # 学习率
lrGamma = 0.98 # 学习率衰减因子
lossValue = 5e-5 # 均方误差允许值
trainLength = int(len(dataset) * trainRatio - ((len(dataset) * trainRatio) % batchSize)) # 保证训练集长度为batch_size的倍数
trainX = dataset[: trainLength, 0]
trainY = dataset[: trainLength, 1]
t = np.linspace(0, dataset[:, 1][-1], len(dataset)) # 时间序列间隔
tForTraining = t[: trainLength]
testX = dataset[:, 0]
testY = dataset[:, 1]
tForTest = t[:]
# 将数组转换为1维
trainXTensor = trainX.reshape(-1, batchSize, inputFeaturesNum)
trainYTensor = trainY.reshape(-1, batchSize, outputFeaturesNum)
# 把数组转化成张量(tensor)
trainXTensor = torch.from_numpy(trainXTensor)
trainYTensor = torch.from_numpy(trainYTensor)
# 把张量传入device(GPU可用时,传入GPU)
trainXTensor = trainXTensor.to(device)
trainYTensor = trainYTensor.to(device)
# LSTM建模
lstmModel = LSTMRNN(input_size=inputFeaturesNum, hidden_size=hiddenSize, output_size=outputFeaturesNum,
num_layers=numLayers)
lstmModel = lstmModel.train()
lstmModel = lstmModel.to(device)
print('LSTM model:', lstmModel) # 打印模型参数
# 均方误差
lossFunction = nn.MSELoss()
# 优化器
optimizer = torch.optim.Adam(lstmModel.parameters(), lr=learningRate)
torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=lrGamma) # 学习率按指数衰减
# 数据训练
for epoch in range(maxEpochs):
output = lstmModel(trainXTensor)
loss = lossFunction(output, trainYTensor)
loss.backward()
optimizer.step()
optimizer.zero_grad()
if loss.item() < lossValue:
print('Epoch [{}/{}], Loss: {:.5f}'.format(epoch + 1, maxEpochs, loss.item()))
print("The loss value is reached")
break
elif (epoch + 1) % 100 == 0:
print('Epoch: [{}/{}], Loss:{:.5f}'.format(epoch + 1, maxEpochs, loss.item()))
# 保存模型系数
torch.save(lstmModel.state_dict(), 'model_params.pkl')
# 读取模型系数
lstmModel.load_state_dict(torch.load('model_params.pkl'))
# 趋势预测
lstmModel = lstmModel.eval() # 加载所有模型结构,调整至测试模型
testXTensor = testX.reshape(-1, batchSize, inputFeaturesNum)
testXTensor = torch.from_numpy(testXTensor)
testXTensor = testXTensor.to(device)
with torch.no_grad(): # 确保预测时梯度不变
predictiveYTest = lstmModel(testXTensor).to(device)
predictiveYTest = predictiveYTest.view(-1, outputFeaturesNum).data.cpu().numpy()
# 结果可视化
resultPlot()
if __name__ == '__main__':
# 1 原始数据处理
# 1.1 获取研究对象车辆的轨迹数据(研究对象不变时,以下数行无需运行)
# itemID = 515 # 选取的车辆编号
# matTotal = loadOrg(itemID)
# dicBuild('TrajectoryFile')
# subDic = 'TrajectoryFile\\' + str(itemID)
# dicBuild(subDic)
# for i in range(len(matTotal)):
# csvBuild(subDic + '\\TrajectoryInter' + str(i) + '.txt', matTotal[i])
# 1.2 读取数据
df = pd.read_csv('TrajectoryFile\\515\\TrajectoryInter1.txt') # 对515号车来说,目前比较有代表性的是1、6号数据
# 2 数据清洗、拆分和结构优化
# 2.1 归一化
scaler = MinMaxScaler()
df['Local_X'] = scaler.fit_transform(df['Local_X'].values.reshape(-1, 1))
df['Local_Y'] = scaler.fit_transform(df['Local_Y'].values.reshape(-1, 1))
# 2.2 查找异常点并删除
index_ = threeSigma(df['Local_X']).index
df = df.drop(index_, axis=0)
# 2.3 构建数组
# 2.3.1 构建轨迹数组并降维
arrayTrajectory = np.array(df[['Local_X', 'Local_Y']]) # 轨迹点数组
arrayDeMean, z, u = methodPCA(arrayTrajectory) # 数据降维处理
# 2.3.2 构建时刻数组
arrayMoment = np.array(df['Global_Time']).astype('float64') # 时刻数组
# 2.4 创建数据集
formatLength = len(z) - (len(z) % 16) # 控制数据集长度为8的倍数,方便设置batch_size
dataset = np.zeros((formatLength, 2)) # 创建空数组以便接收数据
dataset[:, 0] = arrayMoment[: formatLength] # x: 时间指标
z = scaler.fit_transform(z.reshape(-1, 1)) # 降维后轨迹数组的归一化
zOneDim = z.reshape(-1)
dataset[:, 1] = zOneDim[: formatLength] # y: 轨迹指标
dataset = dataset.astype('float32')
# 2.5 创建差值数据集(计算差值前的数据集预测效果较好,暂不运行)
# dataset = np.diff(dataset, axis=0)
# 3 数据训练与结果输出
trainCore(dataset)





