0 问题描述
本报告用于解答如下问题:
0.1 客流条件
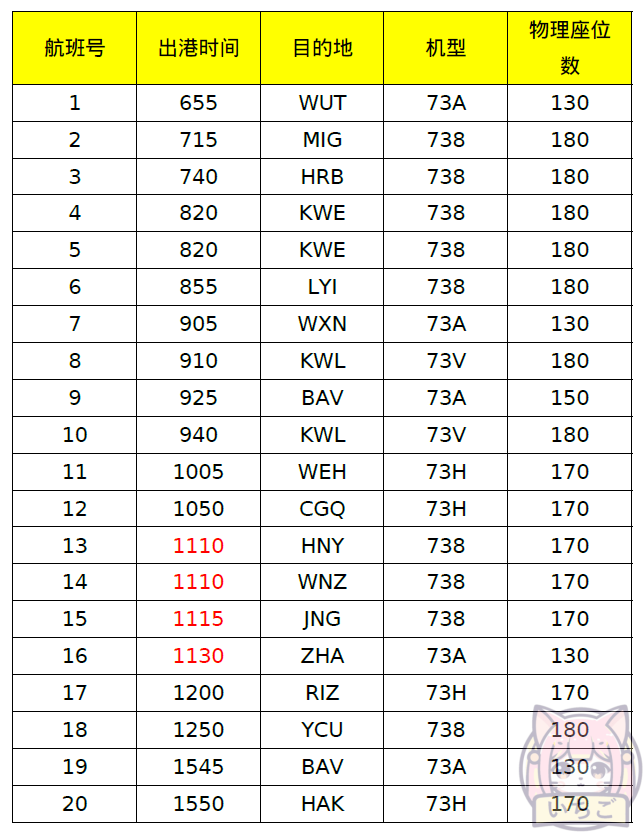
下表为A岛全天值机航班计划,假设上座率均为100%,如规定航班起飞前40分钟停止值机,请在前期资料检索基础上确定早上7:00-9:00的客流到达规律。
0.2 客流服务选择
假设离港客流在人工值机柜台办理值机人数占总人数的60%,每个值机柜台单位时间服务旅客数量服从负指数分布,顾客平均服务时间为3分钟(不区分行李是否托运)。
0.3 值机柜台开放策略
值机A岛柜台总数11个。整个A岛只有一个排队,排队区域采取蛇形排队。各时段柜台开放数量的方案如表所示:

0.4 服务需求
按照机场服务标准:95%的国内经济舱旅客值机手续排队及办理时间应不超过10 min。
0.5 开放问题
当前柜台开放方案,请评估其服务效用。
当前方案是否满足服务要求?如不满足,应如何优化排队(单个队伍或多个排队)和柜台开放策略(分时段开放数量),使之满足服务要求,又能够尽可能降低服务成本。(考虑分时段柜台数对顾客人数的适应关系;柜台开放数量无法实时调整,最小调整间隔为15分钟)
服务成本按照每个柜台的开放时间进行计算,结果为各柜台服务成本(单位为人*分钟)之和。
1 模拟客流到达规律
查阅资料可知,对于有固定截止时间的客流,其随时间变化的到达规律呈现先缓慢增加,到达某一时刻后增速明显加快,之后迅速增加至到达高峰,在截至时间前的某一时刻又迅速减小的趋势。
为将这一客流到达规律用分布函数拟合,以便后续建模分析,可以考虑使用Gumbel分布(I类广义极值分布)拟合乘客到达时刻与停止值机时刻的差值。Gumbel分布的概率密度函数如图1所示,和正态分布相比,其特性为呈现一定的偏态,概率密度函数的极值点一侧变化较陡,另一侧变化较缓,因此对客流到达规律可以取得不错的拟合效果。

对Gumbel分布的参数进行标定时,需要先依据经验给客流到达规律设定一些基础规则,如:平均提前60分钟办理检票(即提前100分钟到机场);只剩不到10分钟办理检票的(即提前50分钟以内到机场,易出现无法登机情况)占统计学意义上的小概率0.5%。
参数标定的过程利用蒙特卡洛模拟进行,让计算机对一定范围内的参数进行筛选,输出最符合上述基础规则的参数,最终得到的结果是位置系数μ=0.488,尺度系数β=0.193。在这一Gumbel分布的基础上建立乘客到达时间生成模型(列表arriveTimeList中存储了每一个研究对象到达机场的时刻,以早上7时作为时刻零点):
# 乘客到达时间生成函数:Gumbel分布
def arriveTimeGenerate(checkTime, seatNums):
# 构造一个默认位生成器
rng = np.random.default_rng()
arriveTimeList = []
for i in range(seatNums):
# 遵循一定的基础规则构建gumbel分布:
# 蒙特卡洛模拟标定的结果:loc=0.488, scale=0.193
arriveTime = rng.gumbel(loc=0.488, scale=0.193, size=None)
# 生成时间的单位:秒
arriveTimeList.append(checkTime - int(arriveTime * 3600))
return arriveTimeList在建立到达时间模型后,再将所有的研究对象以一定的格式输入模型,以获取早高峰的乘客到达时间序列:
# 只研究8:20至10:50出港的航班,再往后的航班旅客在研究时间段到达率极低(经过多次模拟,其到达率低于0.5%),对结果的影响几乎不存在
departureTimeList = [820, 820, 855, 905, 910, 925, 940, 1005, 1050]
seatNumList = [180, 180, 180, 130, 180, 150, 180, 170, 170]
passengerTimeList = []
for i in range(len(departureTimeList)):
arriveTimeList = arriveTimeGenerate(timeInvert(departureTimeList[i]), seatNumList[i])
for item in arriveTimeList:
# 筛出7-9点到达的乘客:班次乘客总数为1520人,这样筛选得到1190人左右
if 0 <= item <= 7200:
# 在人工柜台办理值机的人数占60%
if np.random.rand() <= 0.6:
# 利用Gumbel分布已经将登机失败的概率降到了极低(经过多次模拟,未出现登机失败的情况),可以将所有班次旅客的到达时间直接合并分析
passengerTimeList.append(item)
# 正序排列
passengerTimeList = sorted(passengerTimeList)2 模拟服务规律
在上一节的客流到达模拟中,已经随机生成了60%研究对象的到达时刻列表,现在往列表中添加预计服务时间的信息。由于每个值机柜台单位时间服务旅客数量服从负指数分布,考虑到旅客样本较大(约700人),为尽量保证服务时间的精确度,可以用正态分布替代泊松分布确定服务时间,将服务时间的精度用秒数表示。具体的服务时间生成模型为:
# 服务时间生成函数:泊松分布
def serveTimeGenerate(passengerTimeList):
rng = np.random.default_rng()
passengerList = []
for item in passengerTimeList:
# 用正态分布更精细地模拟泊松分布随机数,可以精确到秒
serveTime = rng.normal(loc=3, scale=1)
# 防止出现过大和过小的极端情况扰乱结果
if serveTime > 5:
serveTime = 5
elif serveTime < 1:
serveTime = 1
passengerList.append([item, round(serveTime * 60 // 1)])
return passengerList在建立服务时间模型后,再将该特征添加至乘客到达时间序列中,得到完整的早高峰乘客特征序列:
# 生成完整的乘客特征序列
passengerList = serveTimeGenerate(passengerTimeList)
# 用直方图描述乘客到达时间分布
plt.hist([passengerList[i][0] for i in range(len(passengerList))], bins=100)
plt.show()由此生成乘客到达时间分布直方图,如图2所示。图2展示的是上述随机生成模型中绝大部分时候出现的情况。图中蓝色和橘色柱形分别为早高峰时间20等分、100等分后每个时段的到达乘客数。可以粗略看出乘客到达数最高的是7:00-7:25(图中时刻0-1500)以及7:40-8:15(图中时刻2400-4500)这两个时段。

3 模拟柜台开放策略
将原始的开放方案用矩阵形式进行表示:
# 柜台开放方案更新时刻及其对应个数,把结束时间7200也写入
# 原始开放方案
planCheckPoint = [[0, 3], [1800, 5], [4800, 3], [7200, 0]]例如:[0, 3]表示方案起始时间为0时刻(即早上7:00),一共3个柜台处于开放状态;[7200, 0]表示方案起始时间为7200时刻(即研究时段的终点9:00),一共0个柜台处于开放状态。
4 服务台数量变化的排队模型
建立排队模型的主要逻辑为:首先解析输入模型的柜台开放策略,通过策略内容划分出各时段内的乘客特征序列,再对该时段内的序列进行排队处理,计算出每个乘客的逗留时间(排队时间与服务时间之和)并输出。
排队处理的思路为:以各服务台所有的空置开始时刻为记录节点,以乘客到达时刻为判定节点,每次乘客到达先判断是否存在空置的服务台,有则将该服务台的空置时刻变为乘客到达时刻与服务时间之和(即延后到这次服务结束),没有则把最近的空置时刻与乘客到达时刻之差作为排队时间,再将该空置时刻变为其与服务时间之和;当服务台数量发生变化时,尽量继承之前的空置时刻(即从大到小继承,减少误差)。
# 排队算法
def originAnalysis(planCheckPoint, passengerList):
# 筛选出timeRange内的到达乘客样本
def timeSeg(passengerList, timeRange):
passengerInRange = []
for item in passengerList:
if timeRange[0] <= item[0] <= timeRange[1]:
passengerInRange.append(item)
else:
if item[0] > timeRange[1]:
break
return passengerInRange
# 按时间顺序进行排队和服务,返回逗留时间(排队时间 + 服务时间)
def timePushForward(startTime, counterNum, passengerInRange):
counterEnptyTime = [startTime for i in range(counterNum)]
# 记录乘客的排队和服务时间之和
sumTime = []
for item in passengerInRange:
# 以服务台空置时刻为核心展开算法,避免研究队长
# 先将空置时刻列表正序排列,方便查找最小值
counterEnptyTime = sorted(counterEnptyTime)
# print(counterEnptyTime, item)
# 如果存在某服务台空置时刻小于等于乘客到达时刻:不需要排队
if counterEnptyTime[0] <= item[0]:
# 计算该服务台的下次空置时刻
counterEnptyTime[0] += item[1]
sumTime.append(item[1])
# 反之需要排队
else:
# 时刻推移到空置时刻出现时,计算下次空置时刻
addTime = counterEnptyTime[0] - item[0]
counterEnptyTime[0] += item[1]
sumTime.append(item[1] + addTime)
return sumTime
passengerTimeSum = []
for i in range(len(planCheckPoint) - 1):
timeRange = [planCheckPoint[i][0], planCheckPoint[i + 1][0]]
counterNum = planCheckPoint[i][1]
passengerInRange = timeSeg(passengerList, timeRange)
sumTime = timePushForward(timeRange[0], counterNum, passengerInRange)
for item in sumTime:
passengerTimeSum.append(item)
return passengerTimeSum5 服务效用评估
5.1 原始方案的服务效用
服务效用依照如下所示的方法进行计算:
# 效用计算函数
def utilityAnalysis(passengerTimeSum, planChenkPoint):
checkNum = 0
for item in passengerTimeSum:
if item <= 600:
checkNum += 1
print('不超过10min的比例: ', checkNum / len(passengerTimeSum))
serveExpense = 0
for i in range(len(planCheckPoint) - 1):
serveExpense += (planChenkPoint[i + 1][0] - planChenkPoint[i][0]) * planChenkPoint[i][1]
print('柜台服务成本: ', serveExpense)由此得到原始方案的服务效用为

即:逗留时间不超过10min的比例为6.7%,柜台服务成本为27 600 / 60 = 460人分钟。因此原始方案无法满足需求。
经分析,即使在当前所有服务台均满载的情况下(即11个柜台在早高峰2小时持续工作),能提供的服务时间为1 320min,而早高峰时旅客到达人工柜台的数量取700人时,需要的服务时间期望值为2 100min,即当前要满足95%旅客逗留时间不超过10min这一需求,必须考虑适当增加柜台总数。
5.2 排队系统及服务方案优化
首先确定队伍数量。队伍数量的增加可能提高对排队空间的利用率,但在单队列采用蛇形排队的情况下,这一效果并非必要。而增加队伍数量会加大各柜台空闲时间的不均衡,对排队系统的整体服务效用为消极作用,因此仍然采用单个队列的方式组织排队系统。
其次则是确定柜台调整时间的大致范围。根据前文对乘客到达能级的判断,必要的柜台数调整时间可能在7:20、7:40、8:15、8:45前后,这几个时间点前后的旅客到达密度发生了较大的变化。
仍然采用计算机多次计算取得最优值的方式,获取优化后的服务效用(为加快求解时间,改变时刻均为60的倍数,即最小单位为分钟)。在满足需求(95%旅客逗留时间不超过10min)之后,通过调整柜台数量、变换时刻,并对超过30min长的时段适当进行拆分,得到最终的优化方案为:
# 新开放方案
planCheckPoint = [[0, 23], [1500, 14], [2400, 27], [3540, 22], [4440, 17], [5340, 13], [6540, 4], [7200, 0]]即:7:00:00-7:25:00设置23个柜台;7:25:01-7:40:00设置14个柜台;7:40:01-7:59:00设置27个柜台;7:59:01-8:14:00设置22个柜台;8:14:01-8:29:00设置17个柜台;8:29:01-8:49:00设置13个柜台;8:49:00以后设置4个柜台(以上数目变化的时间间隔均不小于15min)。
该方案经过1 000次模拟,求出的平均服务效用为:

即:逗留时间不超过10min的比例为95.01%,柜台服务成本为2 187人分钟,已满足需求。
附录:测试代码
if __name__ == '__main__':
# 多次运行取平均值
freqList = []
serveExpense = 0
for epoch in range(1000):
# 只研究8:20至10:50出港的航班,再往后的航班旅客在研究时间段到达率极低,对结果的影响几乎不存在
departureTimeList = [820, 820, 855, 905, 910, 925, 940, 1005, 1050]
seatNumList = [180, 180, 180, 130, 180, 150, 180, 170, 170]
passengerTimeList = []
for i in range(len(departureTimeList)):
arriveTimeList = arriveTimeGenerate(timeInvert(departureTimeList[i]), seatNumList[i])
for item in arriveTimeList:
# 筛出7-9点到达的乘客:班次乘客总数为1520人,这样筛选得到1190人左右
if 0 <= item <= 7200:
# 在人工柜台办理值机的人数占60%
if np.random.rand() <= 0.6:
# 利用Gumbel分布已经将登机失败的概率降到了极低,可以将所有班次旅客的到达时间直接合并分析
passengerTimeList.append(item)
# 正序排列
passengerTimeList = sorted(passengerTimeList)
# 生成完整的乘客特征序列
passengerList = serveTimeGenerate(passengerTimeList)
# 用直方图描述乘客到达时间分布
# plt.hist([passengerList[i][0] for i in range(len(passengerList))], bins=20)
# plt.hist([passengerList[i][0] for i in range(len(passengerList))], bins=100)
# plt.show()
# 柜台开放方案更新时刻及其对应个数,把结束时间7200也写入
# 原始开放方案
# planCheckPoint = [[0, 3], [1800, 5], [4800, 3], [7200, 0]]
# 新开放方案
planCheckPoint = [[0, 23], [1500, 14], [2400, 27], [3540, 22], [4440, 17], [5340, 13], [6540, 4], [7200, 0]]
# 队伍分析
passengerTimeSum = originAnalysis(planCheckPoint, passengerList)
# 效用评估
# 分析结果:原始方案是不满足要求的,会被连续的大值严重影响
freqInDemand, serveExpense = utilityAnalysis(passengerTimeSum, planCheckPoint)
freqList.append(freqInDemand)
print(np.mean(freqList))
print(serveExpense / 60)




